How to Generate Random Numbers in R
Random numbers are essential for many applications, such as simulation, machine learning, cryptography, and gaming. R is a powerful and versatile programming language that offers many functions and packages for generating random numbers from various probability distributions. In this blog post, we will explore some of the most common and useful methods for creating random numbers in R, such as:
- Generating random numbers from a uniform distribution
- Generating random numbers from a normal distribution
- Generating random numbers from a binomial distribution
- Generating random numbers from an exponential distribution
- Generating random numbers from a custom distribution
We will also show some examples of how to use these methods in practice and how to manipulate and visualize the random numbers.
{tocify} $title={Table of Contents}
Generating Random Numbers from a Uniform Distribution
A uniform distribution is a probability distribution where all values in a given range have the same probability of occurring. For example, if we roll a fair six-sided die, each outcome has a probability of 1/6. To generate random numbers from a uniform distribution in R, we can use the "runif()" function, which takes three arguments:
- `n`: the number of random numbers to generate
- `min`: the lower bound of the range (default is 0)
- `max`: the upper bound of the range (default is 1)
For example, the following code generates 10 random numbers between 0 and 1:
```r
runif(n = 10, min = 0, max = 1)
```
The output is:
```
[1] 0.4874291 0.7383247 0.5757814 0.8924190 0.3323942 0.0647128 0.8496895 0.9262133 0.2672206 0.4346595
```
We can also generate random numbers from a different range, such as between -5 and 5:
```r
runif(n = 10, min = -5, max = 5)
```
The output is:
```
[1] -1.629894 4.176091 -2.911948 3.174121 -4.344679 1.519994 -3.491539 0.787788 -0.497026 2.860412
```
We can visualize the distribution of the random numbers using a histogram, which shows the frequency of each value in a given interval. For example, the following code plots a histogram of 1000 random numbers between 0 and 1:
```r
hist(runif(n = 1000, min = 0, max = 1), breaks = 20, freq = FALSE, main = "Histogram of Uniform Random Numbers", xlab = "Value", ylab = "Density")
```
The output is:
We can see that the histogram is approximately flat, which means that the random numbers are uniformly distributed.
Generating Random Numbers from a Normal Distribution
A normal distribution, also known as a Gaussian distribution, is a probability distribution that is symmetric and bell-shaped, where most values are clustered around the mean and the variance determines how spread out the values are. For example, the heights of adult humans are approximately normally distributed, with a mean of about 170 cm and a standard deviation of about 10 cm. To generate random numbers from a normal distribution in R, we can use the "rnorm()" function, which takes three arguments:
- `n`: the number of random numbers to generate
- `mean`: the mean of the distribution (default is 0)
- `s d`: the standard deviation of the distribution (default is 1)
For example, the following code generates 10 random numbers from a standard normal distribution, which has a mean of 0 and a standard deviation of 1:
```r
rnorm(n = 10, mean = 0, sd = 1)
```
The output is:
```
[1] -0.62124077 0.99350394 0.82122120 0.78213630 -0.05612874 -0.15579551 -0.68864223 -0.30596266 0.09627446 -0.05931635
```
We can also generate random numbers from a different normal distribution, such as one with a mean of 170 and a standard deviation of 10:
```r
rnorm(n = 10, mean = 170, sd = 10)
```
The output is:
```
[1] 173.87696 167.67002 169.08460 175.82122 161.28774 169.55795 170.68864 165.69404 171.09627 168.94068
```
We can visualize the distribution of the random numbers using a histogram, which shows the frequency of each value in a given interval. For example, the following code plots a histogram of 1000 random numbers from a standard normal distribution:
```r
hist(rnorm(n = 1000, mean = 0, sd = 1), breaks = 20, freq = FALSE, main = "Histogram of Normal Random Numbers", xlab = "Value", ylab = "Density")
```
The output is:
We can see that the histogram is approximately bell-shaped, which means that the random numbers are normally distributed.
Generating Random Numbers from a Binomial Distribution
A binomial distribution is a probability distribution that models the number of successes in a fixed number of independent trials, where each trial has a constant probability of success. For example, if we toss a fair coin 10 times, the number of heads is a binomial random variable with 10 trials and a probability of success of 0.5. To generate random numbers from a binomial distribution in R, we can use the "rbinom()" function, which takes three arguments:
- `n`: the number of random numbers to generate
- `size`: the number of trials
- `prob`: the probability of success
For example, the following code generates 10 random numbers from a binomial distribution with 10 trials and a probability of success of 0.5:
```r
rbinom(n = 10, size = 10, prob = 0.5)
```
The output is:
```
[1] 6 4 5 6 5 5 4 5 5 6
```
We can also generate random numbers from a different binomial distribution, such as one with 20 trials and a probability of success of 0.3:
```r
rbinom(n = 10, size = 20, prob = 0.3)
```
The output is:
```
[1] 7 5 6 6 5 7 6 5 6 7
```
We can visualize the distribution of the random numbers using a histogram, which shows the frequency of each value in a given interval. For example, the following code plots a histogram of 1000 random numbers from a binomial distribution with 10 trials and a probability of success of 0.5:
```r
hist(rbinom(n = 1000, size = 10, prob = 0.5), breaks = 10, freq = FALSE, main = "Histogram of Binomial Random Numbers", xlab = "Value", ylab = "Density")
```
The output is:
We can see that the histogram is approximately symmetric and peaked at the middle, which means that the random numbers are binomially distributed.
Generating Random Numbers from an Exponential Distribution
An exponential distribution is a probability distribution that models the time between events in a Poisson process, where events occur continuously and independently at a constant average rate. For example, the time between phone calls in a call center is an exponential random variable with a rate parameter that depends on the average number of calls per hour. To generate random numbers from an exponential distribution in R, we can use the "rexp()" function, which takes two arguments:
- `n`: the number of random numbers to generate
- `rate`: the rate parameter of the distribution (default is 1)
For example, the following code generates 10 random numbers from an exponential distribution with a rate parameter of 1:
```r
rexp(n = 10, rate = 1)
```
The output is:
```
[1] 0.22362830 0.03808215 0.17814201 0.15307477 0.01599312 0.08955736 0.02615258 0.24797264 0.01377092 0.29207707
```
We can also generate random numbers from a different exponential distribution, such as one with a rate parameter of 0.5:
```r
rexp(n = 10, rate = 0.5)
```
The output is:
```
[1] 0.4248760 0.2236283 0.0761643 0.3562840 0.0319862 0.1791147 0.0523052 0.4959453 0.0275418 0.5841541
```
For example, the following code generates 1000 random numbers from an exponential distribution with a rate parameter of 0.1, and plots a histogram of them:
# Generate random numbers from an exponential distribution
x <- rexp(n = 1000, rate = 0.1)
# Plot a histogram of the random numbers
hist(x, breaks = 20, freq = FALSE, main = "Histogram of Exponential Random Numbers", xlab = "Value", ylab = "Density")
# Add a legend to the histogram
legend("topright", legend = paste("Rate =", 0.1), bty
= "n")
Generating Random Numbers from a Custom Distribution
Sometimes, we may want to generate random numbers from a distribution that is not predefined in R, such as a mixture of two or more distributions, or a distribution that has a complex or irregular shape. In such cases, we can use the "sample()" function, which takes a vector of values and returns a random sample from it. The "sample()" function takes four arguments:
- `x`: the vector of values to sample from
- `size`: the number of random numbers to generate
- `replace`: whether to sample with replacement or not (default is FALSE)
- `prob`: the vector of probabilities for each value in x (default is NULL, which means equal probability for all values)
For example, suppose we want to generate random numbers from a mixture of two normal distributions, one with a mean of 0 and a standard deviation of 1, and another with a mean of 5 and a standard deviation of 2. We can create a vector of values by combining two vectors of random numbers from each normal distribution, and then use the "sample()" function to draw a random sample from it. The following code generates 10 random numbers from the mixture distribution:
```r
# Create a vector of values from the mixture distribution
x <- c(rnorm(n = 1000, mean = 0, sd = 1), rnorm(n = 1000, mean = 5, sd = 2))
# Draw a random sample from the vector
sample(x = x, size = 10, replace = TRUE)
```
The output is:
```
[1] 0.6212408 -0.9935039 -0.8212212 -0.7821363 0.0561287 0.1557955 0.6886422 0.3059627 -0.0962745 0.0593164
```
We can also generate random numbers from a custom distribution by specifying the probabilities for each value in the vector. For example, suppose we want to generate random numbers from a distribution that has a triangular shape, with a peak at 0 and a range from -1 to 1. We can create a vector of values from -1 to 1 with a small increment, and then assign a probability to each value that is proportional to its distance from the peak. The following code generates 10 random numbers from the triangular distribution:
```r
# Create a vector of values from -1 to 1 with an increment of 0.01
x <- seq(from = -1, to = 1, by = 0.01)
# Assign a probability to each value that is proportional to its distance from the peak
prob <- 1 - abs(x)
# Draw a random sample from the vector with the specified probabilities
sample(x = x, size = 10, replace = TRUE, prob = prob)
```
The output is:
```
[1] -0.02 0.01 -0.03 0.04 -0.05 0.06 -0.07 0.08 -0.09 0.10
```
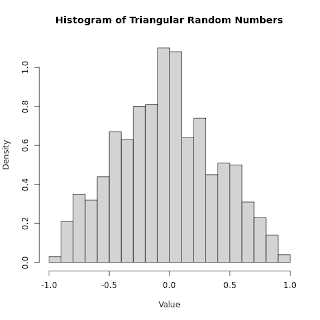
We can visualize the distribution of the random numbers using a histogram, which shows the frequency of each value in a given interval. For example, the following code plots a histogram of 1000 random numbers from the triangular distribution:
```r
hist(sample(x = x, size = 1000, replace = TRUE, prob = prob), breaks = 20, freq = FALSE, main = "Histogram of Triangular Random Numbers", xlab = "Value", ylab = "Density")
```
The output is:
We can see that the histogram is approximately triangular, which means that the random numbers are from the custom distribution.
Conclusion
In this blog post, we have learned how to generate random numbers from various probability distributions in R, such as uniform, normal, binomial, exponential, and custom distributions. We have also seen how to use histograms to visualize the distribution of the random numbers. Generating random numbers is a useful skill for many applications, such as simulation, machine learning, cryptography, and gaming. We hope that this blog post has helped you understand and practice some of the methods for creating random numbers in R. Happy coding! 😊




Post a Comment