Survival analysis, a statistical branch, engages in the scrutiny of time-to-event data. This includes instances such as: time until death; failure--or even recovery. Its application spans across an array of fields including medicine, engineering biology and social sciences.
Kaplan-Meier Curve:
The Kaplan-Meier curve, also known as the product-limit estimator, stands out as a frequently employed and valuable tool in survival analysis. Graphically representing the survival function, it exhibits the probability of enduring until specific time points.
This blog post elucidates the nature of the Kaplan-Meier curve, its calculation methods and interpretation techniques. Additionally, it offers a demonstration on generating Python-based Kaplan-Meier curves with the 'lifelines' library; thereby equipping you to proficiently plot your own.
What is the Kaplan-Meier curve?
The Kaplan-Meier curve: a non-parametric estimator of the survival function--it refrains from assuming any underlying distribution for the survival times. It rests on observed data; these may encompass censored observations, truncated observations, or missing values.
Observations classified as censored are those that either remain unexposed to the event of interest by the study period's conclusion, or have vanished from follow-up. A patient who persists in life post a clinical trial termination, and another patient discontinuing participation for various reasons fall under this censored classification. We glean partial information about survival times from these censored observations since we only ascertain their existence until a specific juncture.
Observations that enter the study after some subjects have already experienced the event of interest are considered truncated. For instance, a patient diagnosed with cancer following the deaths of several others from it would qualify as truncated. These truncated observations might introduce bias in survival analysis by excluding some of the shortest survival times.
Missing values: these lack any information regarding survival times or event status. Consider a patient--one without recorded details of their diagnosis date, death confirmation, or neither status--as an example of such missing data. Further, introduce bias into the survival analysis they might not randomly if we consider missing values; this highlights another potential issue.
Using the product-limit method, the Kaplan-Meier curve incorporates these types of data: it calculates the survival probability at each occurrence of an event--such as death; subsequently, multiplying them together yields the overall survival probability.
The formula for the Kaplan-Meier estimator is:
$$\hat{S}(t) = \prod_{i: t_i \le t} \frac{n_i - d_i}{n_i}$$
where:
- $$\hat{S}(t)$$ is the estimated survival probability at time t
- $$t_i$$ is the time of the i-th event
- $$n_i$$ is the number of subjects at risk just before the i-th event
- $$d_i$$ is the number of events (deaths) at the i-th event
The Kaplan-Meier curve is often plotted as a step function, where the survival probability drops at each event time, and remains constant between the events. The curve starts at 1 (100% survival probability) and ends at 0 (0% survival probability) or the last observed survival probability.
How to create and plot Kaplan-Meier curves in Python?
Import Libraries:
import pandas as pd
from lifelines import KaplanMeierFitter
from lifelines.statistics import logrank_test
import matplotlib.pyplot as plt- pandas: Library for data manipulation.
- KaplanMeierFitter: Part of the lifelines library, used for Kaplan-Meier survival analysis.
- logrank_test: Part of the lifelines library, used for the log-rank test.
- matplotlib.pyplot: Library for plotting graphs.
Sample Data:
data = pd.DataFrame({
'time': [5, 10, 15, 20, 25, 30, 35, 40, 10, 15, 20, 25, 30, 35, 40],
'event': [1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1],
'group': ['Group_A'] * 8 + ['Group_B'] * 7
})This creates a Pandas DataFrame with columns 'time' (time variable), 'event' (binary indicator of an event), and 'group' (group identifier).
Kaplan-Meier Estimation:
kmf = KaplanMeierFitter()
groups = data['group'].unique()
for group in groups:
group_data = data[data['group'] == group]
kmf.fit(durations=group_data['time'], event_observed=group_data['event'], label=group)
kmf.plot_survival_function(show_censors=True, ci_show=True)A KaplanMeierFitter object is created.
The code iterates over unique groups, fits the Kaplan-Meier model for each group, and plots the survival curves.
Log-rank Test:
results = logrank_test(event_times_A=data[data['group'] == groups[0]]['time'],
event_times_B=data[data['group'] == groups[1]]['time'],
event_observed_A=data[data['group'] == groups[0]]['event'],
event_observed_B=data[data['group'] == groups[1]]['event'])The log-rank test is performed to compare survival curves between two groups.
event_times_A and event_times_B are the time variables for each group, and event_observed_A and event_observed_B indicate whether an event occurred.
Print Log-rank Test Results:
print(f'Log-rank p-value: {results.p_value}')Prints the p-value from the log-rank test, indicating the statistical significance of the difference between the survival curves of the two groups.
Plot Formatting:
plt.title('Kaplan-Meier Survival Curve by Group')
plt.xlabel('Time')
plt.ylabel('Survival Probability')
plt.legend(title='Group')
plt.show()Sets titles, labels, legend, and displays the plot of Kaplan-Meier survival curves for each group.Adjustments may be needed based on your specific dataset and analysis requirements.
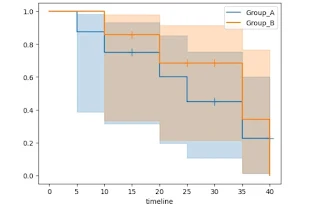
The output plot is:
How to interpret and compare Kaplan-Meier curves?
Kaplan-Meier Curve Visualization:
This plot depicts the estimated survival probability over time:
- X-axis: Represents time (in your specified units, e.g., days, months)
- The y-axis signifies the probability of survival, which ranges from a perfect score of 1—indicating that everyone will survive—to an absolute minimum of 0: signifying that all individuals have already encountered or experienced the event under consideration.
- The step-function line illustrates the estimated probability at each data point: a downward progression of steps signifies either an event occurrence or censoring action.
- Confidence intervals: Shaded areas around the line signify the uncertainty range around the estimated probabilities.
Log-Rank Test:
We can employ the log-rank test to statistically discern the significance of differentiation between two curves; this non-parametric examination compares survival distributions among multiple groups. The null hypothesis of the log-rank test postulates an absence in group differentiations, while its alternative hypothesis suggests a potential variance. Returning a p-value--the probability of observing data under our null hypothesis--this test provides crucial statistical insight. A p-value, typically less than 0.05: it signifies our capacity to reject the null hypothesis and affirm a substantial difference among groups; indeed--it's an indicator of statistical significance.
Advantages of Kaplan-Meier Curves
Survival Analysis Precision
Kaplan-Meier curves, with their primary strength lying in the precise depiction of survival probabilities over time, enhance prediction accuracy by offering a nuanced understanding of event duration. This applies universally: whether it's medical studies or financial analyses--these curves consistently elevate our interpretive grasp on how long until specific events occur.
Accommodation of Censored Data
The Kaplan-Meier curves excel in their ability to handle censored data, a distinct advantage. These robust estimations provide reliable results when we do not know the exact event time, assuring that incomplete information does not compromise our analysis's integrity.
Clear Visualization of Survival Patterns
Kaplan-Meier curves' graphical nature: it allows for a clear, intuitive visualization of survival patterns. The curve's peaks and troughs--providing an overview that is both quick and insightful--illustrate how distinct time intervals witness fluctuations in survival probabilities.
Applications Across Industries
Medical Research and Clinical Trials
Kaplan-Meier curves pivotally assess post-treatment patient outcomes in healthcare. Researchers and clinicians use these curves; they gauge the effectiveness of medical interventions, thus refining treatment protocols.
Finance and Risk Management
To navigate the intricate terrain of risk management, financial analysts rely on Kaplan-Meier curves. These curves enable decision-makers in predicting event probabilities like loan defaults or bankruptcies; thus, empowering them to make informed choices within the realm of finance.
Sociological and Behavioral Studies
Kaplan-Meier curves prove invaluable to sociologists and behavioral scientists in their study of temporal social phenomena: they analyze not only the duration of marriages, but also career trajectories--providing deep insights into human behavior dynamics.
Overcoming Limitations with Kaplan-Meier Curves
Addressing Small Sample Sizes
Kaplan-Meier curves demonstrate exceptional performance in numerous scenarios; however, they might encounter difficulties when dealing with small sample sizes. It is imperative to recognize this limitation: researchers must tread carefully while formulating conclusions from datasets featuring a restricted number of observations.
Integration with Advanced Models
Researchers often integrate advanced models, such as the Cox Proportional-Hazards model, with Kaplan-Meier curves to deepen survival analysis. This synergy facilitates a more comprehensive examination of how various variables impact survival probabilities.
Conclusion
This article introduces the concept and application of Kaplan-Meier curves in survival analysis. It demonstrates construction and comparison methods for these curves with Python's 'lifelines' library, also testing statistical significance using the log-rank test. Utilizing Kaplan-Meier curves provides a powerful, intuitive tool to visualize and analyze survival patterns among various subject groups; this can yield valuable insights for decision-making processes or further research.


Post a Comment